# AtCoder Beginner Contest 182 Tutorial
# Problem A - twiblr (opens new window)
Just output . Time complexity is .
Code (Python 3)
a, b = map(int, input().split())
print(2 * a + 100 - b)
2
# Problem B - Almost GCD (opens new window)
Brute force. Time complexity is .
Code (Python 3)
n = int(input())
a = list(map(int, input().split()))
hi = 0
ans = 0
for i in range(2, max(a) + 1):
cnt = 0
for j in a:
if j % i == 0:
cnt += 1
if cnt > hi:
hi = cnt
ans = i
print(ans)
2
3
4
5
6
7
8
9
10
11
12
13
# Problem C - To 3 (opens new window)
A number can be divided by if and only if the sum of its digits can be divided by .
- , no digits need to be removed.
- , first try to delete one digit that , then try to delete two digits that .
- , first try to delete one digit that , then try to delete two digits that .
Time complexity is .
Code (Python 3)
s = input()
n = int(s)
if n % 3 == 0:
print(0)
else:
a = list(map(int, list(s)))
c = [0] * 3
for i in a:
c[i % 3] += 1
if c[n % 3] >= 1 and len(a) > 1:
print(1)
elif c[3 - n % 3] >= 2 and len(a) > 2:
print(2)
else:
print(-1)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Problem D - Wandering (opens new window)
We can maintain the farthest position , the current position , the prefix sum , and the maximum of prefix sum .
In each round, we first update , then update . It is obvious that we can reach at most in this round, so we will use it to update , and then use to update .
Time complexity is 。
Code (C++)
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
int main() {
int n;
cin >> n;
int a;
ll ans = 0, hi = 0, sum = 0, pos = 0;
for (int i = 1; i <= n; ++i) {
cin >> a;
sum += a;
hi = max(hi, sum);
ans = max(ans, pos + hi);
pos += sum;
}
cout << ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Problem E - Akari (opens new window)
Just put all the light bulbs and the walls into the matrix, then do a -pass scan.
- For each row, from left to right.
- For each row, from right to left.
- For each column, from top to bottom.
- For each column, from bottom to top.
Time complexity is .
Code (C++)
#include <iostream>
#include <vector>
using namespace std;
int main() {
int h, w, n, m;
cin >> h >> w >> n >> m;
int a, b, c, d;
vector<vector<int>> mat(h, vector<int>(w));
for (int i = 0; i < n; ++i) {
cin >> a >> b;
mat[a - 1][b - 1] = 1;
}
for (int i = 0; i < m; ++i) {
cin >> c >> d;
mat[c - 1][d - 1] = -1;
}
for (int i = 0; i < h; ++i) {
bool light = false;
for (int j = 0; j < w; ++j) {
if (mat[i][j] == 1) {
light = true;
} else if (mat[i][j] == -1) {
light = false;
} else if (light)
mat[i][j] = 2;
}
light = false;
for (int j = w - 1; j >= 0; --j) {
if (mat[i][j] == 1) {
light = true;
} else if (mat[i][j] == -1) {
light = false;
} else if (light)
mat[i][j] = 2;
}
}
for (int j = 0; j < w; ++j) {
bool light = false;
for (int i = 0; i < h; ++i) {
if (mat[i][j] == 1) {
light = true;
} else if (mat[i][j] == -1) {
light = false;
} else if (light)
mat[i][j] = 2;
}
light = false;
for (int i = h - 1; i >= 0; --i) {
if (mat[i][j] == 1) {
light = true;
} else if (mat[i][j] == -1) {
light = false;
} else if (light)
mat[i][j] = 2;
}
}
int ans = 0;
for (int i = 0; i < h; ++i)
for (int j = 0; j < w; ++j)
ans += mat[i][j] > 0;
cout << ans;
}2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# Problem F - Valid payments (opens new window)
Actually we need to find the number of tuples that satisfy
and
We can choose from left to right. It is easy to see that, we only need to store each state that can be reached, and the corresponding number of ways. We do not need to store the detailed coefficients.
Since is a multiple of , so after we determine , we need to ensure that the current sum can be divided by . On the other hand, according to the constraint , we only have two choices for each state.
We start from . It seems that there will be exponentional states, but actually, there are at most two states at any time. So the total time complexity is .
# Example
The states in each step are:
As we can see from the example, after each step, all states must be divided by (for the last step, the only valid state is ). Also, the states cannot change more than , e.g., in the first step, we can only go from to or , which are the nearest number that can be divided by to the left and to the right. We cannot go any further because that means we will go more than , and thus violates the rule that both people use the minimum number of coins (because we can use the -Yen coin instead of the -Yen coin).
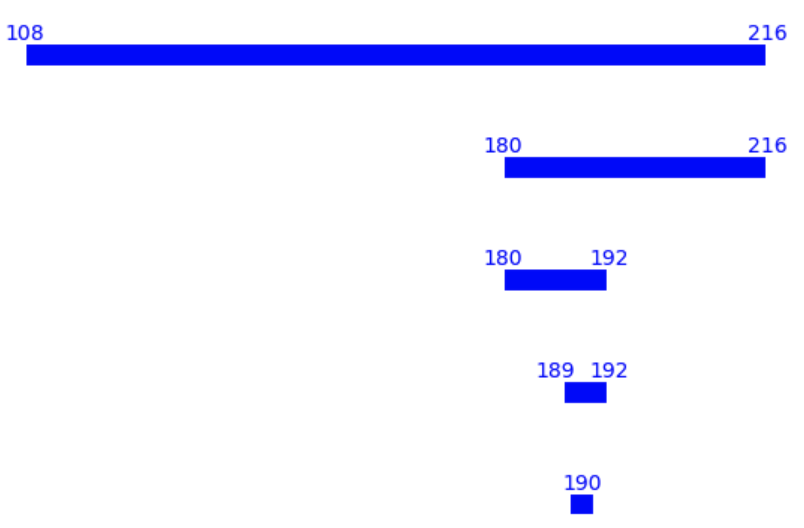
We can also see that, the span is either or exactly for each step.
Code (C++)
#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long ll;
int main() {
int n;
ll x;
cin >> n >> x;
vector<ll> a(n);
for (int i = 0; i < n; ++i)
cin >> a[i];
unordered_map<ll, ll> v;
v[x] = 1;
ll ans = 0;
for (int i = 0; i < n; ++i) {
unordered_map<ll, ll> nv;
for (auto [c, f] : v) {
if (i + 1 < n) {
ll rem = c % a[i + 1];
nv[c - rem] += f;
if (rem > 0)
nv[c + a[i + 1] - rem] += f;
} else {
if (c % a[i] == 0)
nv[0] += f;
}
}
v = move(nv);
}
cout << v[0];
}2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33